The concept of penalized regression as a form of credibility is not new,[1] but it was not formalized into an actuarial methodology until the publication of the monograph “Penalized Regression and Lasso Credibility.” This study provides an actuarial introduction to penalized regression as well as a case study illustrating this new credibility procedure.
When the call for monographs on credibility was announced, my initial thought was to submit an adaptation of an existing paper titled “Credibility and Penalized Regression”[2] that was written by some of my colleagues at Akur8. This paper outlines a mathematical proof of the link between penalization and credibility. The head of the Monograph Editorial Board, Brandon Smith, FCAS, was enthusiastic about the idea of a credibility monograph on penalized regression, but pointed out that a purely mathematical paper would not make a useful monograph. Instead, he recommended that the paper include a case study to show a practical application of lasso credibility. Incorporating a case study was an ambitious expansion, but I believe this addition significantly enhances the paper’s value to the actuarial community.
Rather than a standalone modeling primer, the monograph assumes a basic understanding of GLMs, and builds upon the foundation laid by the CAS Monograph #5, “Generalized Linear Models for Insurance Rating.” It presents penalized regression as an enhancement to GLMs and explains the underlying support for using penalized regression as a credibility measure.
Not every lasso model qualifies as a lasso credibility model. In models configured according to the monograph, the penalty term regulates the credibility standard for the entire model. Increasing the penalty term assigns more credibility to the complement, while decreasing it assigns more credibility to the data. When properly set up, lasso credibility models are extremely quick to build. This approach utilizes the structure of penalized regression to establish a multivariate, likelihood-based credibility procedure.
The main body of the paper offers readers a clear understanding of penalized regression as a credibility model through these and other visualizations. To make the content accessible to a broad audience, the monograph places detailed mathematical proofs and discussions on Bayesian versus Frequentist interpretations in the appendices for those interested in deeper exploration.
The case study follows the methodology an insurer might use when building new models for a commercial auto line of business. We build a series of unpenalized GLM, lasso and lasso credibility models on data representing an insurer’s countrywide book as well as on subsets representing large, medium, and small U.S. states. When reviewing each model, we point out the benefits and drawbacks of each technique as well as what performs well or poorly on this particular iteration of simulated data. These use cases show how lasso credibility allows a modeler to blend the state’s experience with a complement of credibility provided by the countrywide model during the modeling process. By following the modeling guidelines laid out in the monograph, we reach the (expected) result that the credibility assigned to the state-specific experience varies with the state’s size, higher for larger states and lower for smaller ones. Instead of analyzing traditional metrics like deviance, Gini or p-values, the monograph discusses modeling results through the lens of credibility and actuarial appropriateness.
Countrywide models (extremely credible data)
Unsurprisingly, splitting signal between a complement and the data (lasso/lasso credibility) is not materially different from assigning full credibility to the data (unpenalized GLM) on highly credible data such as with countrywide data. This portion of the case study is rather straightforward with no surprises.
Large state data (highly credible data)
Large state GLM and lasso models are quite similar and stable in segments with high exposure, but lasso and lasso credibility approaches begin to show improvement in segments with low exposure. Even on this large dataset, there are small segments that benefit greatly from an appropriate complement of credibility. The use of a complement allows the lasso credibility model to outperform our comparison GLM. (See Table 1.)
Medium state data (moderately credible data)
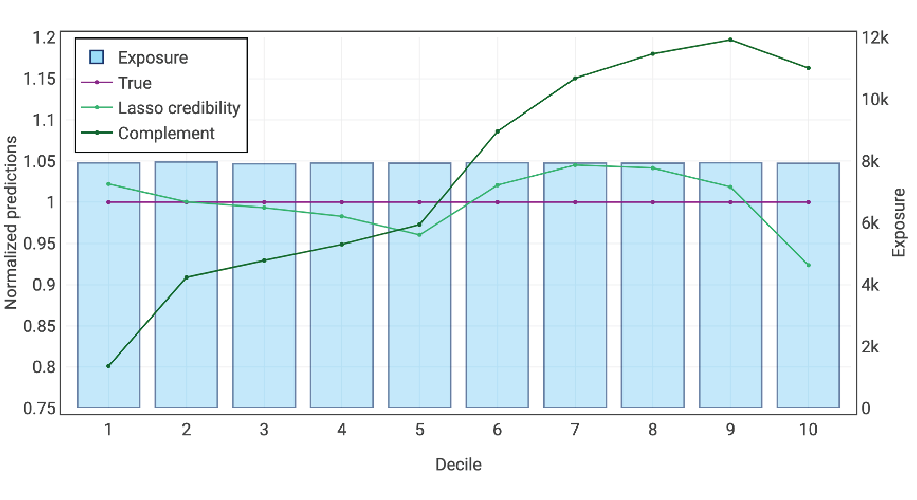
Moderately credible data shows more material advantages for the lasso credibility approach. In the univariate chart below, first note the GLM relativity, which gives 100% credibility to the data. All but one of these coefficients are significant, and an actuary may choose to file and implement these relativities directly. The complement represents an alternative relativity, perhaps the existing rates or a countrywide model. lasso credibility uses penalized regression’s existing fitting process to calculate a credibility-weighted factor that considers all other variables’ fit in the model. We can’t strictly calculate an “assigned credibility” due to the fact that this model takes into account correlations between predictors. Instead, the model must be interpreted through both statistical and actuarial considerations. (See Table 2.)
Small state data (low credibility data)
On this size of data, a GLM is entirely unstable. An insurer would implement their countrywide model rather than spending significant modeling resources to produce a sub-optimal GLM. However, a lasso credibility model not only can be easily fit to this small dataset — it outperforms the countrywide model. (See Table 3.)
This result showcases the true power of the lasso credibility approach: lasso credibility greatly reduces the data requirements and time requirements for successful predictive modeling.
You probably have many questions after reading this article, as I have intentionally omitted many details and assumptions underlying the case study and lasso credibility. The full monograph is available on the CAS website, and the case study code will be available on the CAS GitHub.[3] I encourage you to check it out!
Thomas Holmes, FCAS, is the coauthor with Mattia Casotto of Monograph #13. Holmes is head of U.S. actuarial data science for Akur8.
Table 1.

Normalized double lift chart comparing GLM and lasso credibility results on holdout data. The flatter the line, the better the model represents the true underlying risk relativities in the data.
Table 2.

Univariate chart for industry code showing exposures, modeled relativities and the true underlying risk relativity. In this chart you can see how lasso credibility is producing estimates both informed by fully credible relativities (GLM) and the complement of credibility.
Table 3.
Normalized double lift chart comparing the countrywide model to the small state lasso credibility model on holdout data. The flatter the line, the better the model represents the true underlying risk relativities in the data.