Given the simple equation below, where the pattern of nested operations on the right-hand side continues ad infinitum, what is the exact value of x?

Competition Between Widget Manufacturers
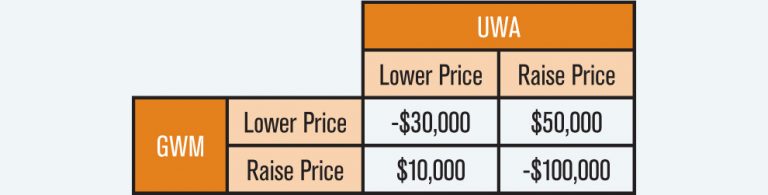
In this puzzle, two widget companies, General Widget Makers (GWM) and United Widget Alliance (UWA), compete. Every day each company can choose to either raise or lower its price; the price cannot be unchanged; the price change must be fixed for the day. The companies cannot collude or cooperate or share knowledge before they announce their daily price changes. Neither company will ever exit the market, as shutdown costs more than any possible loss. The profit to GWM (equivalently the loss to UWA) for any day is as follows:

The question was, what should each company be advised to do?
This is a zero-sum game without a min-max saddle point. Such a saddle point would exist if each company could pick its own single, fixed strategy, always lowering or always raising prices, and these strategies would simultaneously minimize the maximum loss for each company. But each company can pursue a random mixed strategy, lowering p% of the time and raising 100% – p% of the time, that is stable in the min-max sense. If p is the probability that GWM will raise and G is GWM’s profit in $1,000s, then if UWA raises then G = -100p +50(1-p) = 50 – 150p and if UWA lowers then G = 10p -30(1-p) = -30 +40p. This is shown in the chart, top right.
Obviously, GWM will minimize its maximum loss, independent of what UWA does, when 50 – 150p = -30 +40p that is when p =8/19, leading to G = -13.1579
If q is the probability that UWA raises and U is the profit to UWA in $1,000s, then if GWM raises U = 100q – 10(1-q) and if GWM lowers U = -50q + 30(1-q). The corresponding chart is shown bottom, right.
UWA minimizes its maximum loss, regardless of what GWM does, when 100q – 10(1-q) = -50q + 30(1-q) that is when q = 4/19, leading to U = 13.1579. So, if p =8/19 and q =4/19 then G = –U and neither company can change anything to decrease its maximum expected loss.
Solutions were also submitted by Bob Conger, Rob Kahn and Gregory Scruton.
Know the answer? Send your solution to ar@casact.org.
AR Puzzle Editor Jon Evans is president of Convergent Actuarial Services, Inc. in Delray Beach, Florida.











