You are a scientist on a research ship positioned over the Mariana Trench, which is 11 kilometers deep. Four super-strong solid spheres are securely tied to the deck. You plan to untie them and gently push them off the ship.
- Sphere A has density 10 percent lower than the density of water at the bottom of the Trench.
- Sphere B has density 10 percent higher than the density of water at sea level.
- Sphere C has density 10 percent higher than the density of air at altitude 100 kilometers (official boundary of space).
- Sphere D has density 10 percent lower than the density of air at sea level.
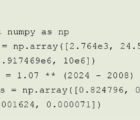
Without looking up any specific empirical physical measurements, based on general principles of physics, roughly and qualitatively speaking, at what altitude above or depth below sea level will each of the spheres end up? Can you look up some actual empirical measurements and estimate quantitatively these altitudes and depths? Intuitively, does this suggest it should be easier to control the altitudes of airships or the depths of submarines, or are they both equally difficult to control? How consistent is this intuition with the history of airship and submarine technologies?
More Refined Pricing
It turns out that Tony’s pricing formula P(m,n) is not more refined at all and must be exactly $300 for all values of m and n. This is because the averaging constraint P(m,n) = (P(m+1,n) + P(m-1,n) + P(m,n+1) + P(m,n-1))/4 is the defining condition for a function on the lattice Z2 to be harmonic. Harmonic functions that are bounded, either in maximum or minimum, must be constant. This is a version of Liouville’s theorem, although the more familiar versions apply to continuous harmonic functions or continuous analytic functions. Furthermore, this can be generalized to Zd where d is any non-negative integer. So, even with more than two rating factors, Tony’s formula would still charge a flat $300 in all cases.
Unfortunately, a proof of Liouville’s theorem for all positive harmonic functions on Zd appears to be intrinsically rather complicated. This was an unexpected surprise. I first saw reputable references in mathematical literature that this version of the theorem was true.
I expected some relatively simple proof to exist, since several other versions of the theorem do have fairly simple proofs, but to no avail. I continued my search.
The simplest approach to the proof outline that I know of and reasonably trust can be downloaded here.
Absolutely no one submitted solutions to this puzzle.
