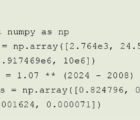
Martha only invests in Stock A or in Stock B, and only in one of these stocks at a time. The market for each of these stocks, respectively, only trades at a single price for each day, which is — with equal probability — either 105 percent or 95 percent of the previous day’s price for that stock. There are no sequential autocorrelations or sequential cross-correlations between price changes, and no cross-correlation for price changes on the same day. Whenever the stock Martha holds goes up five percent and the other stock goes down five percent on the same day, Martha sells the stock she holds and invests all the money in the other stock. Assume that fractional shares are allowed, that there are no dividends, no bid/ask spreads and no commissions, and that Martha has no insider information.
Martha starts with $10,000 invested entirely in Stock A. After 1,000 days of trading, what is the expected value of Martha’s stock? What are the 5th and 95th percentiles of the value?
What would the answers be if the same-day price changes for the two stocks have a +50 percent cross-correlation? What if the cross-correlation is -50 percent?
Buoyancy
Water, for the most part, behaves like an incompressible fluid, with its density independent of how much pressure it is under. So, it is reasonable to expect water to have about the same density from sea level all the way to the bottom of the Mariana Trench. Air is clearly less dense than water, but behaves mostly like a highly compressible fluid. It is general knowledge that air rapidly gets thinner with increasing altitude, until it becomes effectively a vacuum in space, several hundreds of kilometers above the Earth.
Consequently, it is reasonable to expect that:
- Sphere A, with density 10 percent lower than the density of water at the bottom of the trench, should float on the surface of the ocean.
- Sphere B, with density 10 percent higher than the density of water at sea level, should sink all the way to the bottom of the Mariana Trench.
- Sphere C, with density 10 percent higher than the density of air at altitude 100 km (official boundary of space), should float in the air lower than 100 km, but not dramatically lower — maybe at 80 km or 90 km.
- Sphere D, with density 10 percent lower than the density of air at sea level, should float in the air, but not dramatically higher than sea level — maybe at a few hundred meters or so.
Googling a little bit reveals that water at the bottom of the Mariana Trench is only about 5 percent denser than at sea level, where its density is about 1,000 kg/m3. Similarly, the density of air at sea level is about 1.225 kg/m3. So, our intuition about Spheres A and B is exactly correct. Furthermore, the density of air at 1,000m is about 10 percent lower at about 1.112 kg/m3. So, Sphere D should float at around 1,000m altitude, about in line with intuition.
The density of air declines roughly exponentially. At altitude 70 km it is about 0.00008283 kg/m3, and at 80 km it is about 0.00001846 kg/m3. So given the rate of exponential decline at these high altitudes, to get to 10 percent higher density than at 100 km, we need to use the constant a = ln(0.00001846/0.00008283)/(10,000 m) = -0.00015/m and then solve for 1.1 = e-0.00015d. This leads to d = -635 m, which is the approximate descent from 100,000 m to get a 10 percent increase in density. So, Sphere C should float around a little bit above 99 km, quantitatively higher than our intuition but qualitatively about the same.
All this would suggest that controlling the altitude of an airship should be much easier than controlling the depth of a submarine. A big change in the density of an airship only leads to a relatively small change in altitude and, consequently, its altitude should be very stable. However, a submarine’s depth is so unstable that a 5 percent increase in its density would cause it to sink all the way to the bottom of the deepest part of the ocean.
However, this intuition is completely in opposition to the historical outcomes for these technologies. Despite the constant difficulty of keeping a stable submerged depth for a submarine, submarines are still in widespread use (mainly by the military, who spend days or weeks at a time submerged) more than a century since their initial development. Some of these military submarines are powered by nuclear reactors and are enormous, such as the 24,000 ton Russian Typhoon submarines. However, submarines have experienced relatively few incidents of accidental sinking.
In contrast, the gigantic airships of the early 20th century, like the ill-fated LZ 129 Hindenburg, which was almost three football fields long, proved to be extremely difficult to control. They almost invariably crashed and were almost totally withdrawn from civilian and military use prior to World War II. A few dramatically smaller, simpler blimps remain in service today, typically used in short distance low altitude advertising roles. Even these blimps have to make emergency landings occasionally due to control problems.
A solution was submitted by Chris Norman.
