Craig, a genetic engineer, is trying to sequence a DNA sample from an ancient dinosaur as part of a research grant from a private theme park resort on an island. Craig consults his brother Gary, a statistical modeler, to determine if the sequencing can be completely finished within a year. Craig’s DNA sequencer can read a single linear segment 5,000,000 base pairs long for each hour it is running. The sequencer can only match the linear segments together if they overlap by at least 2,000,000 base pairs. The segments can only be sampled (with replacement) in a completely random way from a long circular strand of dinosaur DNA. The sequencing finishes when every base pair has appeared in at least one sampled segment that can be “spliced together” by matching its overlap with other sampled segments so as to sequence the complete circle of base pairs. Gary responds that there is a 99 percent chance the sequencer will finish within a year. How many base pairs long is the strand of dinosaur DNA?
Buffon’s Sphere Inside a Triangulated Honeycomb
In this problem, all of space is filled with a tetrahedral-octahedral tessellation (or honeycomb). All edge lengths are equal to a constant L. A sphere with radius R materializes at a random point in space. If there is a 50 percent probability that the sphere lies entirely within a single polyhedral cell, what is R/L? More generally, what is the corresponding probability for any R/L?
Puzzle solver Bob Conger answers these questions along the following lines. Every face is shared by a tetrahedron and an octahedron, but an octahedron has eight faces versus four on a tetrahedron, so the space contains twice as many tetrahedrons as octahedrons. Given a constant length L of the sides, the volume of an octahedron is four times that of a tetrahedron.
Therefore, 2/3 of space is filled with octahedrons, and 1/3 with tetrahedrons. Thus, there is a 2/3 probability that the center of the sphere will fall within an octahedron, and 1/3 probability that the center will fall within a tetrahedron.
Next construct another tetrahedron (octahedron) inside each tetrahedron (octahedron) in the tessellation, with the walls of the interior shape being a uniform distance R inside the walls of the exterior shape. If and only if the center of the sphere is within one of these newly constructed polyhedrons, the sphere will be entirely within a polyhedron of the tessellation.
The radius of an inscribed sphere that is tangent to each face of the tetrahedron is L/√24 (or L/√6 for an octahedron). The corresponding radius for a constructed tetrahedron is L/√24-R (or L/√6-R for a constructed octahedron). Note, the constructed radius being >0 is necessary for any possibility that the sphere falls entirely within a tetrahedron (octahedron). In this case the ratio of the volume of a constructed tetrahedron to the volume of an original tetrahedron is (1- (R/L)*√24)3 (or (1- (R/L)*√6)3 for the octahedrons). Therefore, the overall probability of the sphere materializing entirely within a polyhedron is:
(1/3) x { [1-(R/L)*√24 ]3, subject to a minimum of zero }
+ (2/3) x { [1-(R/L)*√6 ]3, subject to a minimum of zero }
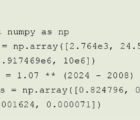
For probability = 50 percent, the solution is, if you can stand going through the formula for a cubic polynomial,
or with simple numerical root finding about 0.06531.
The probability is zero percent when R/L >= 1/√6. As R/L is decreased from this value, the probability continuously rises achieving every value on the open interval (0%, 100%). The probability can be set arbitrarily close to 100 percent by selecting R/L small enough. For example, R/L = .001 produces a probability of approximately 99 percent.
Editor’s Note: Solutions for the July/August 2015 puzzle, “The Darkness between the Stars and the Size of the Universe,” were sent in by Jay Call and Bob Conger.
