A three-dimensional lattice spans all the points with integer-valued coordinates from the extreme diagonal points with minimum integer coordinates (0,0,0) to maximum integer coordinates (L,M,N). Estimate the volume LMN given the following random sample of lattice points:
( 4, 20, 5 )
( 14, 38, 59 )
( 24, 16, 31 )
( 31, 30, 1 )
( 6, 29, 4 )
( 5, 2, 1 )
( 12, 22, 30 )
( 30, 46, 69 )
( 23, 3, 31 )
( 17, 43, 41 )

Extra credit: What do you estimate will be the standard error of your estimate versus the true value of LMN?
Here is a SHA-256 hash that will not help you solve the problem in any way. It includes a message to be revealed when the solution is published, with the values (L,M,N) and LMN used to generate the random sample of lattice points.
88b8448136047d588cfa8cd091a4f0b3d9d0cb7c7808508bf660d515c2719ea5
Know the answer? Send your solution to ar@casact.org.
Combining Squares
Here is a nice step-by-step solution submitted by John Berglund.

We are given two squares, with sides a and b, with a > b > 0. Call the squares A and B.
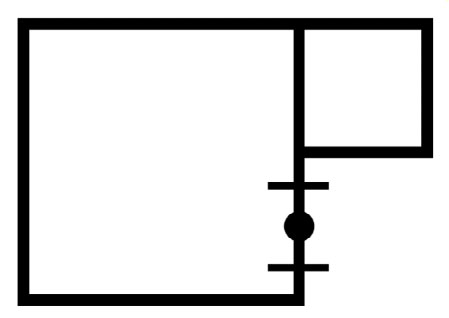
Set square B next to square A. There will be a segment of length a-b along the side of A sticking out below B. Find the midpoint of this segment.
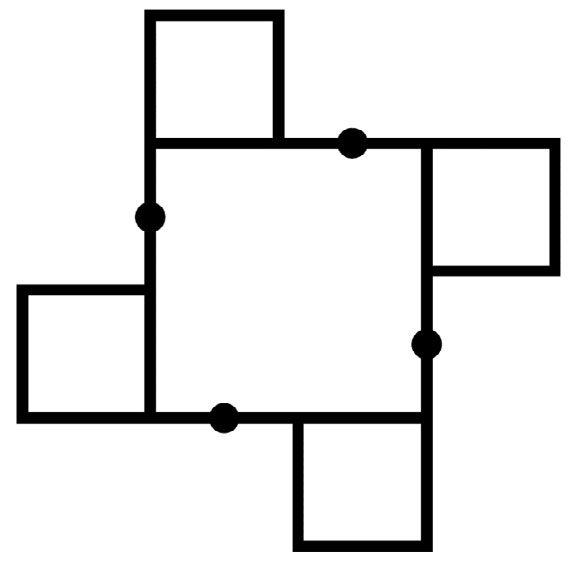
We can repeat this process on each side of square A. (With rotational symmetry.)

We can connect each midpoint to the one opposite. This cuts square A into four identical pieces.
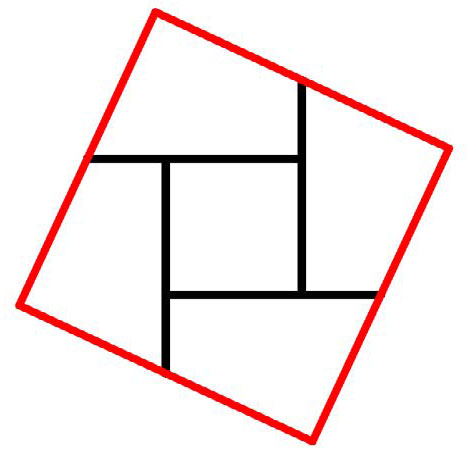
We can arrange the four pieces plus square B to make a bigger square. This is the goal.
Roger Bovard, Bob Conger, Jacob Flisakowski, Jerry Miccolis, Hannah Park, Chris Terrill and Brian Thompson also submitted solutions.
John Berglund also submitted a solution for the January/February 2023 puzzle.












