The dial on a standard combination padlock, the kind often used with gym lockers, is numbered zero to 39. The combination to open it is given by a set of three numbers. For example, if the numbers are 30-39-20, to open, turn right to 30, then turn left all the way around to 30 again and continue to 39, then turn right to 20. However, the mechanism is usually not very exact, and if you use a close combination like 31-38-22, it will still open. Suppose you can be off by up to an increment of two, either to the left or to the right, for each of the numbers and the lock will still open. If you had no idea what the combination was, using the most efficient search strategy, what is the greatest number of combinations you might have to try to open the lock?
Know the answer? Send your solution to ar@casact.org.
Risk Appetites
Kim and Ann initially each have an equal total amount of money. Kim acts so as to maximize the expected squared amount of her total wealth, whereas Ann tries to maximize the expected square root of the amount of her wealth. Kim and Ann can each choose a fraction (from 0 percent to 100 percent) of their initial wealth to gamble on a fair coin flip, with the winner claiming the total amount that both bet. The coin flip is voluntarily negotiated beforehand so that the fraction each of them bets — the fractions need not be equal — is acceptable to the other one. What combinations of betting fractions would be mutually acceptable to them? Do you have an opinion about what specific combination of betting fractions they might settle on?
Solver Clive Keatinge let k be the proportion of Kim’s wealth that she bets and let a be the proportion of Ann’s wealth that she bets, where Kim and Ann start with the same amount of wealth. Kim requires that 0.5(1+a)2+0.5(1-k)2≥1 and Ann requires that 0.5(1+k)0.5+0.5(1-a)0.5≥1. Thus, any combination of betting fractions that satisfies these two inequalities would be mutually acceptable to both of them.
If equality does not hold in the first inequality, then Kim can do better by reducing the proportion that she bets until equality is reached. Likewise, if equality does not hold in the second inequality, then Ann can do better by reducing the proportion that she bets until equality is reached. Thus, a Nash equilibrium requires that equality holds in both inequalities. The only solution to these equations is k=a=0. Keatinge opines that Kim and Ann will likely call the whole thing off.
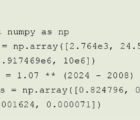
Note that Keatinge’s implicit opinion is that Kim and Ann are noncooperative and consequently cannot achieve an agreement to bet. In contrast, Bob Conger’s opinion is that Kim and Ann would cooperate so that the expected utility (value of money) for both of them is equal and that this utility is maximized, assuming that they both have equal utility of one for their initial amount of money. This occurs around k =100% and a=46.4842%, so that they both achieve an expected utility of 0.5(1+a)2+0.5(1-k)2=0.5(1+k)0.5+0.5(1-a)0.5=1.07288.
My opinion is that Kim and Ann would, along the lines of the Nash arbitration scheme, end up with an agreement that maximizes the product of the gains in their utilities over not betting. This would result in k=100% and a=54.231%, with Kim’s expected utility being 0.5(1+a)2+0.5(1-k)2=1.18936 and Ann’s expected utility being 0.5(1+k)0.5+0.5(1-a)0.5=1.04537. Both would gain, but relative to Conger’s equal utility gain constraint, Kim would be driving a harder bargain out of Ann. Note that the product of their utility gains under Nash arbitration (1.18936-1)(1.04537-1)=0.00859126 is greater than under the equal utility gain constraint (1.07-1)(1.07-1)=0.0049.
Solutions were also submitted by Ernest Lin and Brad Rosin.
