You work at a casino owned by Sheldon. Sheldon presents you with a roulette-like machine that spins around and randomly stops at a number from 1 to n, where n is fixed, each number having equal probability. Sheldon asks you to design a new game where the probability of winning is p. Can you do this? If so, explain how. If not, explain why not?
Rockets Into Deep Space
The key to this puzzle is the famous “Rocket Equation” that you can find in Wikipedia and various other references, but is not very hard to derive by applying calculus to Newton’s Third Law. The momentum of an object with mass M and velocity V is MV. In a closed system, all changes in momentum must sum to 0 by Newton’s Third Law. So when a rocket of total mass M increases its velocity by dV, through burning an infinitesimal amount of rocket fuel dM with exhaust velocity Ve, the equation M dV = – Ve dM holds. If a rocket starts with total mass M0 and weighs Mt after all its fuel is burned, then the total change in velocity it experiences can be expressed by the integral 
since M is changing and Ve is constant.
Rocket booster mass consists of structural mass Ms and fuel mass Mf. Let the probe mass be Mp. When n boosters are fired in parallel M0 = Mp + n(Ms + Mf) and Mf = Mp + n Ms. To simplify calculations, we can choose units of mass so that Mp = 1 and units of velocity so that Ve = 1. Then from the statement of the puzzle we get two equations:
and 
.
These equations appear to not yield an algebraic solution, but numerical methods (like Solver in Excel) lead to the solution Ms = 0.852207 and Mf = 11.4909. The ratio of ΔV from firing n boosters in parallel to ΔV firing just one booster is 
. As n → ∞ this ratio increases and asymptotically approaches a limit of 
. So Wernher tells Walter that it is impossible to double the velocity of the probe, or even just to increase it by 36 percent, by adding boosters to be fired in parallel.
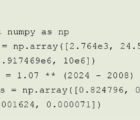
If a series of boosters is fired in sequence, discarding each after being fired, then ΔV from firing the kth from last booster is 
. See Table 1.
Consequently, Wernher tells Walter that 10 boosters fired in sequence will be needed to double the velocity of firing just one booster.
Solutions were also submitted by Bob Conger, Rob Kahn, Clive Keatinge, Jerry Miccolis and Brad Rosin.
